Timothy O'Neill i Karl Seelig
Termin "squircle" to połączenie słów "square" i "circle". Wygląda jak kwadrat z zaokrąglonymi rogami. Matematycznie kształt ten znany jest jako superelipsa. Jeśli chodzi o projektowanie szablonów SMT, często stosuje się luźniejszą definicję, a rzeczywisty kształt jest znany jako zaokrąglony kwadrat - generowany przez oddzielenie czterech ćwiartek koła i połączenie ich linią prostą.

Jak się okazuje, squircle to skuteczny kształt maksymalizujący zarówno objętość pasty lutowniczej w ciasnych przestrzeniach, jak i poprawiający wydajność transferu.
Właściwości przysłon kwadratowych
Konstrukcja typu squircle łączy w sobie pozytywne cechy zarówno okrągłych, jak i kwadratowych przysłon.
Funkcje przysłony kołowej
Ze względu na ich gładką, zaokrągloną konstrukcję, okrągłe otwory nie mają narożników zachodzących na podkładkę ani martwych stref pasty. Jednak znacznie trudniej jest uzyskać wystarczającą ilość pasty w ciasnych przestrzeniach przy użyciu okręgów. Wynika to z faktu, że powierzchnia koła o danej średnicy jest mniejsza niż powierzchnia kwadratu o tej samej długości boku (używając wzorów na powierzchnię koła i powierzchnię kwadratu: (π/4)d2 < d2).
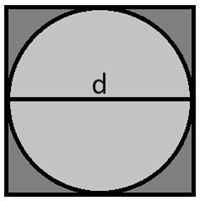
Dodatkowo, okręgi mają równe napięcie powierzchniowe na całej średnicy otworu. Podczas separacji może to zwiększyć ilość pasty lutowniczej, która pozostaje w otworze. Wyobraź sobie bańkę mydlaną na płaskiej powierzchni; równe napięcie powierzchniowe zapewnia jej stabilność. Ta sama cecha zniechęca pastę do opuszczania okrągłego otworu.
Cechy kwadratowej przysłony
Kwadrat ma nieodłączną zaletę maksymalizacji objętości pasty w ciasnych przestrzeniach. Jednak podczas drukowania pasty lutowniczej cząsteczki mają tendencję do aglomeracji w ostrych rogach otworów, co powoduje większe różnice między poszczególnymi depozytami. Jest również prawdopodobne, że zmienność ta wzrośnie z czasem, jeśli skuteczność wycierania szablonu zmniejszy się, a nagromadzenie pasty wzrośnie.
Kwadraty mają z natury większą powierzchnię niż okręgi o tym samym głównym wymiarze, więc powinny osadzać więcej pasty, ale jeśli te narożniki chwytające pastę zachodzą na krawędzie podkładki, powodują również problemy z uszczelnieniem, które mogą dodatkowo powodować duże odchylenia.
Przysłony kwadratowe
Squircle łączy korzyści objętościowe kwadratowych otworów z korzyściami uwalniania pasty z zaokrąglonych kształtów, co pozwala również uniknąć obszarów gromadzenia się pasty. Zapewnia to najlepsze z obu światów w niezwykle wymagającej części procesu drukowania.
Eksperymentalne porównanie kształtów przysłony
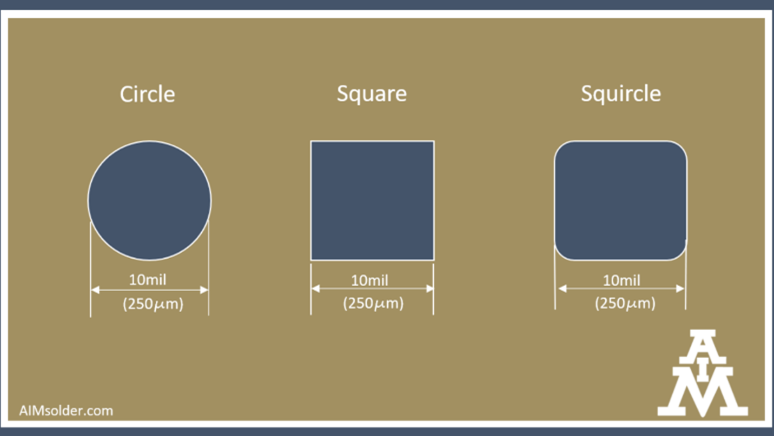
Szeroko zakrojone testy druku w laboratorium aplikacji AIM w Juarez w Meksyku, przy użyciu szablonu zawierającego kwadratowe, okrągłe i kwadratowe kształty apertury, potwierdzają mocne argumenty przemawiające za kwadratem jako rozwiązaniem wielu wyzwań związanych z drukiem. Testując apertury o tym samym głównym wymiarze (średnica lub długość boku) i podobnych proporcjach powierzchni, byliśmy w stanie bezpośrednio porównać wydajność transferu i rzeczywiste objętości depozytu.
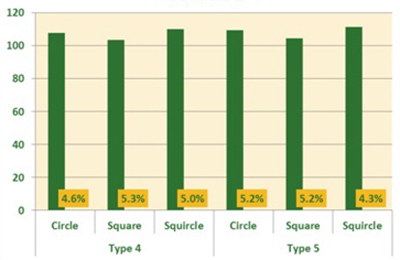
RYSUNEK 4 przedstawia zmierzone sprawności transferu i obliczone współczynniki zmienności dla każdego typu przysłony. Należy zauważyć, że wydajność transferu jest nieco niższa w przypadku kwadratu niż koła, ale tylko o kilka punktów procentowych. Kwadrat ma również nieco większą zmienność w przypadku pasty typu 4 i odpowiada danym pasty typu 5. Kwadrat konsekwentnie ma najwyższą szybkość transferu i porównywalną lub niższą zmienność niż kwadraty i koła.
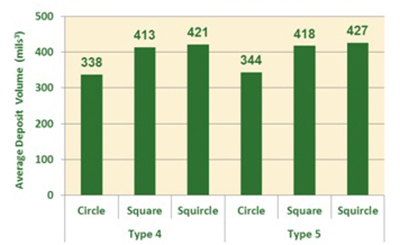
RYSUNEK 5 przedstawia średnią objętość zdeponowaną przez każdy kształt otworu. Należy zauważyć, że chociaż kwadrat wykazywał niższą wydajność transferu, jego większa powierzchnia skutkowała większą objętością niż okrąg. Z kolei wiewiórka zdeponowała największą objętość ze wszystkich otworów. We wszystkich przypadkach pasta typu 5 konsekwentnie wytwarzała marginalnie wyższe objętości, ale nie na tyle, aby uzasadnić przejście na nią w środowisku produkcyjnym, w którym pojawiłyby się problemy związane z kosztami, oddzielnym przechowywaniem i ponownym rozpływem.
Uwagi końcowe
Należy zauważyć, że w tych eksperymentach szybkość transferu jest bardzo wysoka, a zmienność bardzo niska w porównaniu z typowymi wynikami podobnych testów drukowania. Testy druku zostały przeprowadzone w idealnym środowisku, przy użyciu szablonu z nanopowłoką polimerową. Rozsądne jest oczekiwanie podobnych trendów w środowiskach produkcyjnych, ale z niższymi szybkościami transferu i wyższymi wskaźnikami zmienności. Rozsądne jest również rozważenie zastosowania nanopowłok na szablonach o wąskich proporcjach powierzchni ze względu na (często udokumentowaną) poprawę jakości, jaką zapewniają.
Zebrane dane, ale nie pokazane tutaj, wskazują również, że wiewiórka jest bardziej odporna na skutki starzenia w temperaturze pokojowej i długich przerw (> 60 min.) między wydrukami.
Chociaż nasze badanie podkreśla potencjał squircle, dalsze badania są uzasadnione, aby zbadać jego zastosowania w różnych warunkach montażu i materiałach. Niemniej jednak, wstępne wyniki są obiecujące, pozycjonując squircle jako realne ulepszenie praktyk projektowania szablonów.
Na podstawie artykułu "Kwadratura koła" opublikowanego pierwotnie w zespole obwodów.